Huygens का सिद्धांत Priciple of Huygens

Huygens का सिद्धांत 

यद्यपि Huygens ने प्रकाश के लिए तरंग सिद्धांत का प्रतिपादन किया, उन्होंने इन तरंगों को माध्यम में विक्षोभ के रूप में ही प्रस्तुत किया था। 

मान लें कि किसी माध्यम में एक बिंदु सरीखा स्रोत S तरंगें उत्पन्न कर रहा है जो सभी दिशाओं में समान रूप से फैल रही हैं। माध्यम में जिस बिंदु पर तरंग पहुँचती है वहाँ का कण कंपन करने लगता है। कहा जाता है कि यहाँ विक्षोभ पहुँच गया। यदि आप S को केंद्र बनाकर एक गोलाकार सतह Σ₁, खींचें, तो इस सतह के सभी बिंदुओं पर के कण एक समय पर एक ही कला में कंपन कर रहे होंगे। ऐसी सतह जिसके सभी बिंदुओं पर एक क्षण पर एक ही कला में विक्षोभ हों, तरंगाग्र (wavefront) कहलाती है। तरंग के चलने की दिशा सदा तरंगाग्र पर लंबवत होती है। प्रकाश के संदर्भ में यह दिशा प्रकाश की किरण को दिखाती है। यदि आप t समय बाद की स्थिति को सोचें, तो ऐसी ही कला के कंपन गोलाकार सतह Σ₂, पर पहुँच जाएँगे, जिसकी त्रिज्या पहले वृत्त की त्रिज्या से vt अधिक होगी। अतः, हम कहेंगे कि तरंगाग्र पहली सतह Σ₁, से दूसरी सतह Σ₂, पर पहुँच गया है। चित्र में ये स्थितियाँ दिखाई गयी है 

तरंगाग्र Σ₂ का बनना Σ₁ पर के कणों के कंपन के कारण हीं हुआ है। एक अर्थ में आप सोच सकते हैं कि तरंगाग्र Σ₂ के बनने के लिए Σ₁, सतह पर के कण ही तरंगों के स्रोत है। Huygens ने इसी मूल धारणा को सिद्धांत का रूप दिया। इस सिद्धांत के अनुसार, जब किसी सतह के किसी बिंदु पर एक तरंगाग्र पहुँचता है, तो वह बिंदु एक द्वितीयक (secondary) स्रोत की तरह व्यवहार करने लगता है तथा उस बिंदु से गोलाकार द्वितीयक तरंगकाएँ (secondary wavelets) निकलने लगती है। बाद के किसी समय पर इन द्वितीयक तरंगिकाओं को स्पर्श करती हुई आगे की दिशा की सतह ही मूल तरंगाग्र की नई स्थिति होगी।

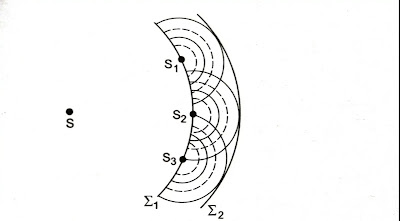
 इस क्लिष्ट प्रतीत होती भाषा को समझने के लिए हम एक सरल उदाहरण देंगे। मान लें एक बिंदु-स्रोत S सभी दिशाओं में तरंग भेज रहा है और Σ₁ एक गोलाकार सतह है, जिसका केंद्र S है (चित्र)। किसी समय t = 0 पर तरंग Σ₁ पर पहुँचती है और Σ₁ एक तरंगाग्र बन जाता है। Huygens के सिद्धांत के अनुसार, Σ₁ के बिंदु S₁, S₂, S₃, आदि द्वितीयक स्रोत (secondary source) बन जाते हैं और गोलाकार तरंगिकाएँ (spherical wavelers) उत्पन्न करते हैं। चित्र में t = 0 से t=t तक की कई तरंगिकाएँ (wavelets) दिखाई गई हैं। मोटे वक्र crest को निरूपित कर रहे है तथा डैश से बने वक्र trough को निरूपित कर रहे हैं। t समय पर S₁, S₂, S₃ से निकली तरंगिकाएँ (wavelets) vt त्रिज्या की गोलाकार सतहे बनाती हैं। अब इन गोलाकार सतहों पर, तरंग के आगे बढ़ने की दिशा में, स्पर्श करती हुई दूसरी सतह खींचें। यह स्पर्श सतह एक बड़ी गोलाकार सतह Σ₂ होगी जिसका केंद्र S पर होगा। यही बड़ी गोलाकार सतह t समय पर नया तरंगाग्र होगा। 

Huygens का सिद्धांत वस्तुतः एक विधि है, जिससे आप एक तरंगाग्र (wavefront) से बाद के समय का तरंगाग्र बना सकते हैं। ऊपर के उदाहरण में हमने पहली सतह Σ₁, ऐसी ली थी कि S से चलता तरंगाग्न एक साथ Σ₁, के सभी बिंदुओं पर पहुँचा था, अर्थात Σ₁, स्वयं एक तरंगाग्र था। यह आवश्यक नहीं है। आप कोई भी सतह लेकर उसे Σ₁, की तरह इस्तेमाल कर सकते हैं। मूल तरंगाग्र अलग-अलग समय पर Σ₁, के विभिन्न बिंदुओं पर पहुँचेगा और द्वितीयक तरंगिकाएँ (secondary wavelets) अलग-अलग समय पर इन स्थानों से उत्पन्न होंगी। फिर भी, आप आगे के किसी समय पर इसपर स्पर्श सतह बनाकर नए तरंगाग्र की स्थिति पता कर सकते हैं।